奇妙的Pairing Function及实际用途

在实际项目里，我们经常需要把二维坐标 (x, y)、或两个整型键合成一个“唯一”的整型键，方便做哈希表/数组索引；又希望能在需要时还原回原来的两个键。这样一个反直觉的需求真的有解决方案吗？“配对函数”（Pairing Function）隆重登场。

什么是 Pairing Function？

配对函数把两个非负整数 (x, y) 唯一映射到一个非负整数 z，并且可以从 z 唯一地解回 (x, y)。

本文只介绍最常用的形式：Cantor 配对函数。

Cantor 配对函数

把 (x, y) 编码为单个整数：

z = (x + y) * (x + y + 1) / 2 + y

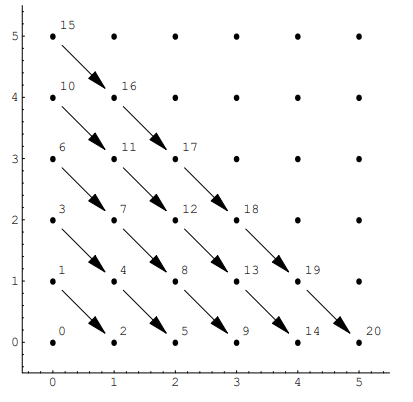
直觉：先把同和的点按“斜对角”分组（x + y = s），每个 s 有 s + 1 个点；(x + y) * (x + y + 1) / 2 是第 s 条斜对角之前累计点数（一个三角形数），再加上本条里的偏移 y，就得到唯一的 z。

从 z 解回 (x, y)：

1. 找到最大的 w 使 w*(w+1)/2 <= z ；
2. 令 t = w*(w+1)/2；
3. y = z - t；
4. x = w - y。

这四步就是把 z 定位到它所在的那条斜对角，再求出在该斜对角上的具体位置。

代码实现

下面给出简单可用的实现（x,y 为非负整型）。注意：

• 使用 64 位整型保存编码结果：当 x,y 为 32 位时，z 可能超过 32 位范围。
• 反解中的平方根对超大数值可能有浮点误差，必要时可用二分法寻找 w（通常 64 位下用 sqrt 已够用）。
• Cantor 仅适用于非负整数；处理负数请先做 I2N/N2I 映射。

// C#
public static ulong CantorPair(uint x, uint y)
{
    ulong s = (ulong)x + y;
    return s * (s + 1) / 2UL + y;
}

public static (uint x, uint y) CantorUnpair(ulong z)
{
    ulong w = (ulong)Math.Floor((Math.Sqrt(8.0 * z + 1) - 1) / 2.0);
    ulong t = w * (w + 1) / 2UL;
    uint y = (uint)(z - t);
    uint x = (uint)(w - y);
    return (x, y);
}

要处理有符号整数？常见做法是先把 int 双射到非负整数，再套用上面的编码：

I2N(n) = n >= 0 ? 2n : -2n - 1
N2I(n) = n % 2 == 0 ? n/2 : -(n/2) - 1

在游戏开发里的用法

• 网格/Tile 索引：把 (row, col) 合成数组/哈希键，省去嵌套容器。
• 空间哈希：把 (cellX, cellY) 合成键存入 unordered_map/Dictionary。
• 路径搜索与“已访问”集合：把坐标对映射成唯一标识。
• 组合状态或复合主键：如 (entityId, componentType)。

进一步阅读

• 更“优雅”的另一种形式（Szudzik）：Elegant Pairing